Introduction to Using R for Evaluating Census Data

INTRODUCTION

The Census Program conducted by Statistics Canada provides a snapshot of Canada’s demographic, social and economic characteristics through the Census of Population and Census of Agriculture (Statistics Canada, 2016a).  Demographic and statistical data from the census can be aggregated, analyzed and used to for decision-making such as public planning and federal funding allocation (Statistics Canada, 2016a). The census is a pivotal component of Canada’s statistical infrastructure and provides data necessary for social and economic research to answer questions about Canadian society (Green and Milligan, 2010; Dillon, 2010). The census is particularly useful for change detection research, and observing patterns over time by investigating past and present data (Dillon, 2010). In general, the census provides the most detailed body of information about the Canadian population, which can be used to answer questions such as:

How does median household income differ across provinces?
Has the proportion of the population in low income changed?

The first census of a confederated Canada was completed in 1871 in 98 colonial and regional districts, and included 211 questions including population questions on occupation, age, sex and religion (Statistics Canada, 2011). Under the Constitutional Act, a census would take place every tenth year no later than May 1st (Statistics Canada, 2011).  Fast forward to 1971, the 100th year anniversary of the first census of Canada, the Statistics Act was introduced and a population census became required every five years, and was now completed by questionnaire instead of interview (Statistics Canada, 2011).  The 1971 census also saw the division between short-form and long-form census. Two-thirds of Canadian households would receive the short-form census which included basic population and housing questions, while the remaining one-third of households would receive a long-form census that included an additional 50 questions (Statistics Canada, 2011).

The Conservative government replaced the long-form sentence in 2011 with the voluntary National Household Survey (NHS), citing the long-form census as being too intrusive (Ditchburn, 2010). The NHS had an overall response rate of 68.6% in 2011, compared to the long-form census return rate of 93.5% in 2006. This raises many issues because non-response is non-random, which results in response bias that is no longer representative of the population (Green and Milligan, 2010). The non-response bias is a result of respondents being significantly different from non-respondents, a problem which was minimized in mandatory long-form census due to high return rate (Veall, 2010). The Liberal government reinstated the long-form sentence after taking office in 2015, and the long-form census was implemented in addition to the short-form census in the most recent census, which was completed May 2016 (Voices-Voix, 2011)

Census data is used by government, industry, and institutions to derive population information in a variety of topics. Mitrou et al. (2014) used Canadian census data in addition to census data from Australia and New Zealand to study social determinants of health and inequity in Indigenous peoples. The study relied on census data related to education, employment and income for the study age cohort of 25-29 years. In Canada, the Mitrou et al. (2014) found that the unemployment gap between Indigenous and non-Indigenous people who hold at least a bachelor’s degree in 2006 was 6.6%, and for other countries it was as high as 11.0%. Compared to statistics from 1981, the data did not show a significant improvement, which led Mitrou et al. (2014) to conclude that Indigenous populations are just as disadvantaged in the areas of employment and income as they were in 1981. Census data is used extensively in research from fields like public health, where it can be a tool to  answer questions about populations in topics such as environmental pollution (Jerrett et al., 2009), physical activity and obesity (Eaton et al., 1994; Gordon-Larsen et al., 2006), and disease prevalence (Fung et al., 2014). 

The use of census data in this study will be to observe population density in the Capital and Cowichan Valley Regional Districts of southern Vancouver Island and familiarize with the concept of spatial autocorrelation through using global and local statistics to evaluate spatial patterns in population density distribution.

Spatial Analysis and Spatial Autocorrelation

Spatial analysis is a component in geographical analysis which can be used to describe and explain patterns that can be observed in the places around us. Spatial analysis allows us to ask and answer questions about places and place relationships in areas such as transportation, environmental monitoring, urban planning, conservation, public health and agriculture (Beale and Mitchell, 2015). Spatial autocorrelation is a type of spatial analysis that allows for measurement of similarities or differences between an object and other objects nearby. Positive spatial autocorrelation, or clustering, is when objects that are closer together are more similar, while negative spatial autocorrelation or dispersion is when objects that are closer together are more dissimilar. This is a powerful tool for spatial analysis and can be used to explain geographic patterns by characterizing the distribution of subjects and the patterns of their attributes (ESRI, n.d.). In understanding spatial autocorrelation, it is important to first familiarize with geography Waldo Tobler’s First Law of Geography (GIS Geography, 2017):

“Everything is related to everything else, but near things are more related than distant things.”

The measurement is spatial autocorrelation is to confirm whether Tobler’s law holds true for the subject matter being observed. Spatial autocorrelation can be measured through various global and local statistical methods including: Moran’s I, Geary’s C, and Getis’ G (Sawada, 2009). Global statistics derives characteristics about an entire dataset, while local statistics demonstrate the variability within the dataset. Using statistical methods of measuring spatial autocorrelation can be applied to census data to answer questions like:

Are dual-income households more common in larger urban centres than smaller ones?
Do people from rural areas retire earlier?

Continue through the basic R tutorial below to take the first steps in learning how to use census data to conduct spatial analyses! Begin by installing R on your PC or laptop from here.

COLLECTING AND MAPPING CENSUS DATA

Select 2016 census data products can be accessed and downloaded from Statistics Canada’s website and new products will continue to become available. The data used for this study includes cartographic boundary shapefiles, available here and population and dwelling count available here. Aggregate dissemination area was the boundary type used, which is a delineation based on areas that have a population count of 5000 to 15 000 people (Statistics Canada, 2016b).

To begin, open R and install the packages that will be used for the tutorial:

1. PLYR: For splitting, applying, and combining data (Wickham, 2016).
2. DPLYR: For manipulating datasets and a continuation from the PLYR package (Wickham, 2014).
3. Spdep: Spatial dependendence package containing functions for creating weighting schemes from polygons and points, and summarizing these using statistics and models. Includes tests for spatial autocorrelation including Moran’s I, Geary’s C, Getis Ord and other global and local methods (Bivand, 2017a).
4. GISTools: Mapping and spatial manipulation tools used to create choropleth maps and legends (Brunsdon and Chen, 2014).
5. Raster: Tool package used to read, write, manipulate, analyze and model gridded spatial data and able (Hijmans, 2016).
6. Maptools: Tool package for reading and manipulating spatial objects such as ESRI shapefiles (Bivand, 2017b).

Use the function library() to load the functions into R for use.

library(plyr)
library (dplyr)
library(spdep)
library(GISTools)
library(raster)
library(maptools)

To map and use the data files on R, set the working directory to the location where the files are saved and open the files through either a data input function directly (ex. read.csv) or by assigning the data input function to a new object.

Setwd (“Users/angel/geography/lab3”)
dissem <- shapefile (“lada000b16a_e.shp”)

The dissemination area shapefile contains all of Canada, but we are only focusing on the Capital and Cowichan Valley Regional Districts. Select just these two regions and assign a new object containing the selection: 

dissem.sub <- dissem[dissem$CDNAME %in% c(‘Capital, “Cowichan Valley),]

Now call the census population data csv file, assign it to a new object. Using value matching and pattern matching/replacement functions format the population data.

census.16 <- read.csv(“T1701EN.csv”, check.names = FALSE)
names(census.16) <- gsub(“[[:space:]]|[[:punct:]]”, “_”, names(census.16), fixed = FALSE)
names(census.16) <- gsub(“__”, “_”, names(census.16), fixed = TRUE)
names(census.16) <- gsub(“__”, “_”, names(census.16), fixed = TRUE)
census.16 <- census.16[,-12]
census.16 <- census.16[,-grep(“french”, names(census.16))]

This step creates a new object which replaces punctuation and spaces with underscores to assure that our data does not contain any values that might confuse R and create errors. After formatting data and removing unwanted punctuation,select the columns to be used: geographic code, 2016 population, total private dwellings, and 2016 population density. This step removes the clutter of unnecessary data columns from the csv file. To do this, create an object and select the data columns that will be used. 

census.16 <- census.16[,names(census.16) %in% c(“Geographic_code”, “Population_2016”, “Total_private_dwellings_2016”, “Population_density_per_square_kilometre_2016”)]

To map the census attribute data with the geographic shapefile, the data is merged by geographic code. In the shapefile the geographic code is named ADUID. To merge the population information as attribute data for the shapefile, rename the geographic code column in the census.16 object with ADUID using the name function. Then merge the shapefile with the population data using the merge function by assigning a new object and remove any missing data values. 

names(census.16)[1] <- “ADAUID”
crd.data <- merge (dissem.sub, census.16, by = “ADAUID”
crd.data <- merge(dissem.sub, census.16, by = “ADAUID”)
crd.data <- crd.data[!is.na(crd.data$Population_2016),]

Using functions from the GIS Tools library, a choropleth map can be drawn. A choropleth map is a popular type of thematic map that represents different classifications of values with distinct colour classes (Pennsylvania State University, n.d.). In our map, we want to create a choropleth that uses six classification categories, assigned as different colour shades to population density ranges for our study area of Capital and Cowichan Valley Regional District. The function choropleth will take three arguments: a spatial polygon object (crd.data), a mapping variable (PopDen) and a shading scheme for classification (shades). First assign the population density to a new vector PopDen and the shading scheme to the object shades. The chorolegend function creates a legend for the choropleth map. The function takes arguments for x and y coordinates, which will tell it where to plot the legend, and also an argument for the shading scheme. The output generated is a choropleth map of population density for each dissemination area within the study area.

PopDen <-crd.data$Population_density_per_square_kilometre_2016
shades <- auto.shading(PopDen, n=6, cols = brewer.pal(6, ‘Oranges’))
choropleth(crd.data, PopDen, shades)
choro.legend(3864000, 1965000, shades)

The output is a six class choropleth map of population density in the Capital and Cowichan Valley Regional Districts. The highest population density dissemination areas look to be mainly in the Greater Victoria area, where the values are the darkest. There are also some darker areas of higher population density around Ladysmith and Duncan.

Neighborhood Weights Matrix

When evaluating spatial data, it is important to consider and take into account spatial weights (Bivand, 2017a). A spatial weight matrix is a method of summarizing the spatial relationships between units in an area of observation. In the case of this study, it looks at the spatial relationship between different dissemination areas on the Capital and Cowichan Valley Regional Districts (Smith, 2015). The purpose of creating a spatial weights matrix is to quantify the spatial influence that neighbor values have on adjacent units so values assigned to units are representative of these interactions (Smith, 2015). 

To create a weight matrix with the census data, neighbors and non-neighbors need to be determined for each point, to assign weight values. The method of determining neighbors in R used is the function poly2nb which constructs a neighbor list from polygon list. This function uses queen’s case by default, but rook’s case will also be used for neighbor weighting. Queen’s case designates neighbours based on sharing a common edge or vertex, while rook’s case only considers a shared edge.  Queen’s and rook’s case neighborhood weighting are examples of contiguity weighting, where  weight is given to adjacent neighbors. Spatial weights matrices can be created through other methods of neighbor determination including: k-nearest neighbor weights, radial distance weights, and power distance weights (Smith, 2015). It is outside the scope of our study to create different types of neighbors, but descriptions and code for other methods of creating neighbors can be found here.

Use poly2nb and plot functions to generate queen and rook neighbors for the aggregate dissemination areas and plot both neighbor files on the census shapefile.

crd.nb <- poly2nb(crd.data)
plot(crd.data)
plot(crd.nb, coordinates(crd.data), add = TRUE, col = “red”)

Crd.nb2 <- poly2nb (crd.data, queen = FALSE)
plot(crd.data, border = “lightgrey”)
plot(crd.nb, coordinates(crd.data), add = TRUE = “red”)
plot(crd.nb2, coordinates(crd.data, add = TRUE, col = “yellow”, lwd=2)

Now create a weights list and summary from the neighbor weighting. Print the list. 

Crd.lw <-nb2listw(crd.nb, zero.policy= TRUE, style = “W”)
print.listw(crd.lw, zero.policy = TRUE)

The results show that 356 nonzero links are weighted in 86 regions to generate weighted population density values for the aggregate dissemination areas map. The average number of links is approximately 4, and the percentage of nonzero weights is 4.8%. Looking at the neighbors in the queen’s case and rook’s case maps, it can be identified that most contiguous neighbors in the Capital and Cowichan Valley Regional Districts can be classified by rook’s case(yellow). The maps produced by creating a neighborhood weights matrix can be used to visualize which values are considered neighbors, but the usefulness of this part of the tutorial is demonstrated in the next section when the neighborhood weight matrix is applied to the population density map. 

Mapping Lagged Means

By creating a neighborhood weights matrix, a lagged means map can be generated. A lagged means map calculates how different the z-score for each dissemination area is from the mean z-score, and in combination with the population density data, can be used as a method of visualizing population density that is weight adjusted based on spatial influence of neighboring values. The purpose of generating a lagged means map is to allow the spatial influence of neighbors to be accounted for in the visualization of data. 

To create a choropleth where influence of neighbor weight is applied  to population density values , we first need to lag the population density based on the weights matrix. This procedure is similar to generating the unweighted population density map and uses most of the same functions. An additional function lag.listw is used to generate the new data frame to plot. 

PopDen.lagged.means <- lag.listw(crd.lw, PopDen, zero.police=TRUE)
shades2 <- auto.shading(PopDen.lagged.means, n=6, cols = brewer.pal(6, ‘Oranges’))
choropleth(crd.data,PopDen.lagged.means, shades2)
Choro.legend (3864000, 1965000, shades 2)

The new choropleth map produces a thematic visualization of population density across the study area of Capital and Cowichan Valley Regional Districts, but now as a lagged means map that is adjusted for spatial weights. The population density values are adjusted based on neighbor weights, so more similar neighbors (based on z-scores, not significance) are adjusted for more proportionally similar population density values.

A side-by-side comparison of the unweighted and weighted population density maps demonstrates the change in population density values when neighbor weights are accounted for. The classification has been reassigned for the weighted map to better suit the spatial data. The upper boundaries of the weighted map are lower values than the upper boundaries for the unweighted map. Looking at some of the values that have been reclassified, the two largest dissemination areas seen on the maps have been reassigned from under 58 people per square kilometer classification to 49-220 people per square kilometer.

Global Moran’s I

Global Moran’s I is the most common method of measuring spatial autocorrelation, which it calculates using both point and attribute data (ESRI, n.d.). The purpose of Global Moran’s I is to determine if points that are closer together have more similar attributes. This is done by looking at attributes between value i and its neighbors j and conducting an inferential test (z-test) to determine if there is a random distribution or if the data displays positive or negative spatial autocorrelation. Global Moran’s I, as its name indicates, is a global statistic method that generates one value which summarizes the entire dataset. The value derived is an inferential statistic which can be tested for significance by calculating a z-score and p-value. In a hypothesis test for Global Moran’s I the null hypothesis is that the spatial distribution of values assessed display complete spatial randomness (CSR).

It is important to recognize that the defining part of the Moran’s I statistic is the determination of neighbors and neighbor weighting. This importance can be better understood through the formula for calculating the Moran’s I statistic. The calculation is a standardized value of the following products: (1) the weight determining relationship of the observed value and neighbors, (2) the difference between the observed value (i) and the mean, and (3) the different between neighbors (j) and the mean. To determine significance a z-test is performed which is the expected Moran’s I subtracted from the calculated Moran’s I, and divided by the variance.

In R the function moran.test will test for spatial autocorrelation by taking a spatial weights matrix argument in the form of a weights list (listw) and a numeric vector which is the same length as the neighbors list. The list that will be used is the one generated previously (crd.lw) and the vector is the census population density (PopDen).

mi <- moran.test(PopDen, crd.lw, zero.policy = TRUE)
mi

This code assigns the moran test function to an object (mi) using the population density and spatial weights matrix list, as well as the argument zero.policy. When assigned TRUE zones without neighbors will be assigned a lagged value of zero. The code then prints the results of the moran test. The results include the Moran I statistic, p-value, standard deviation, expected Moran I, and variance. The following values were derived:

Moran I statistic standard deviation: 9.0328
P-value <2.2 data-preserve-html-node="true" x 10¹⁶
Moran I statistic: 0.739092892
Expected Moran I statistic: -0.011764706
Variance: 0.006909813

The Moran I statistic calculated for the dataset is much larger than the expected Moran’s I statistic. This suggests that the population density values for the Capital and Cowichan Valley Regional Districts do not display CSR, but are positively autocorrelated. Moran’s I values range typically from -1 to 1 where a value of zero represents no spatial autocorrelation and negative and positive values represent negative and positive spatial autocorrelation, respectively. The Moran I statistic that was derived from the R Moran test resulted in a value of 0.74, which is closer to one and suggests positive spatial autocorrelation. This is supported by the p-value, which is less than 2.2 x 10-¹⁶ suggesting that there is less than 0.001% likelihood that a Type I error is committed, and that a true null hypothesis has been rejected.

To conceptualize the Moran I value derived we will generate a range of potential Moran I values in R by defining our own function moran.range. 

Moran.range <- function(lw) {
wmat <- listw2mat(lw
return (range(eigen((wmat + t(wmat))/2)$values))
}

moran.range(crd.lw)

The moran range derived is -1.479792 to 1.504245, which is larger than the typical range explained above of -1 to 1.  To confirm if the population density is spatially autocorrelated, perform a z-test to confirm the p-value derived and significance. Call the values that were returned from the Moran’s I test (Moran I statistic, expected Moran I statistic, variance) for use in the z test and assign it to a new object. As shown above in formula figure, the calculation of a z-score for a Global Moran’s I is computed as the expected Moran’s I value subtracted from the calculated Moran’s I value, and then divided by the variance. In R, assign this formula to a new object. 

ztest <- (mi$estimate[1]-mi$estimate[2]/mi$estimate[3])

The z-test value calculated is 108.6654. Assuming a two-sided test with a confidence interval of 99%, the critical z-scores would be -2.58 and 2.58. The calculated z-score lays much farther to the right of the critical value for normal distribution. A z-score of 108.6654 and p-value of < 2.2 x 10^-16 support the conclusion that the pattern of population density in dissemination areas of Capital and Cowichan Valley Regional Districts is positively spatial autocorrelated.

Local Moran’s I

The drawback of a global statistic is that it only derives one value informing the user whether data is or is not spatially autocorrelated. If the data is spatially autocorrelated, the Global Moran’s I is unable to determine where correlations are. The Local Moran’s I can be used to calculate Moran’s I values for each observation based on spatial weight which can be used to identify where local spatial patterns exist. Local Indicators of Spatial Association (LISA) like Local Moran’s I can be used for two purposes: (1) as an indicator of hot spots and (2) detect the outliers and the influence that individual locations have on the global statistic (Anselin, 1995). The sum of all Local Moran’s I should be approximately equal to the Global Moran’s I statistic (Anselin, 1995).

The Local Moran’s I function localmoran is similar to the Global Moran’s I function moran.test, as it takes a spatial weights list and a vector the same length as the weights list. Run this function by assigning it to a new object which takes the population density vector and the queen’s case neighbor weighting list. Then print the object for review.

lisa.test <- localmoran(PopDen, crd.lw)
lisa.test

Printing  the object lisa.test gives the calculated Local Moran’s I, expected Local Moran’s I, variance, z-score, and p-value for each individual cell. This output is similar to the data output from printing the Global Moran’s I result, but in the Local Moran’s I, these values are derived for individual cells, rather than one set of values that defines the entire dataset.

To summarize all the data produced by the Local Moran’s I test visualize it on the study area map. To create a choropleth based on the Local Moran’s I values follow the procedure used to generate the lagged means map by designating a shading scheme, generating a map, and adding a legend. Use [,1] to select column that contains calculated Local Moran’s I values.

lisa.shades <- auto.shading (c(lisa.test[,1], -lisa.test[,1]), cols=brewer.pal(5, “PRGn”))
choropleth(crd.data, lisa.test[,1], shading=lisa.shades)
choro.legend(3860000, 1965000, lisa.shades, fmt=”%6.2f”)

The Local Moran’s I choropleth is able to show which dissemination areas have similar Moran’s I values, but it is not based on significance. The positive Moran’s I values are indicative of having neighbors that have similar high or low values while the negative Moran’s I values are indicative of having  neighbors with dissimilar values. While the Local Moran’s I choropleth may be used to infer where clustering is occurring, to confirm this, a choropleth map that uses p-values rather than Moran’s I values should be produced to confirm significance. This can be done by making a few small changes to the choropleth map code for creating a Local Moran’s I value choropleth.

plisa.shades <- auto.shading(lisa.test[,5], n=5, cutter = sdCuts, cols =rev(brewer.pal(5, “PRGn”)))
choropleth(crd.data, lisa.test[,5], plisa.shades)
chorolegend(3860000, 1965000, plisa.shades)

The p-value map for Local Moran’s I shows areas with smaller p-values in green and larger p-values in purple. The green values represent areas where a Type 1 error is less likely to have occurred, and can be used to confirm that the dark green areas in the Local Moran’s I map are more similar, or clustered (p<0.17). The values that are purple or white have a larger p-value and indicate areas where there is a greater likelihood of committing a Type 1 error by rejecting the null hypothesis. This means that the areas that are white or purple may not be concluded to be areas of positive spatial autocorrelation.

Mapping the Local Moran’s I values and Local Moran’s I p-values is useful for assessing spatial autocorrelation because it allows us to identify where clusters are happening within the data. While the Global Moran’s I calculations allowed us to conclude that there is positive spatial autocorrelation in our dataset, the Local Moran’s I calculations and mapping allowed us to determine the specific dissemination areas where the positive spatial autocorrelation are.

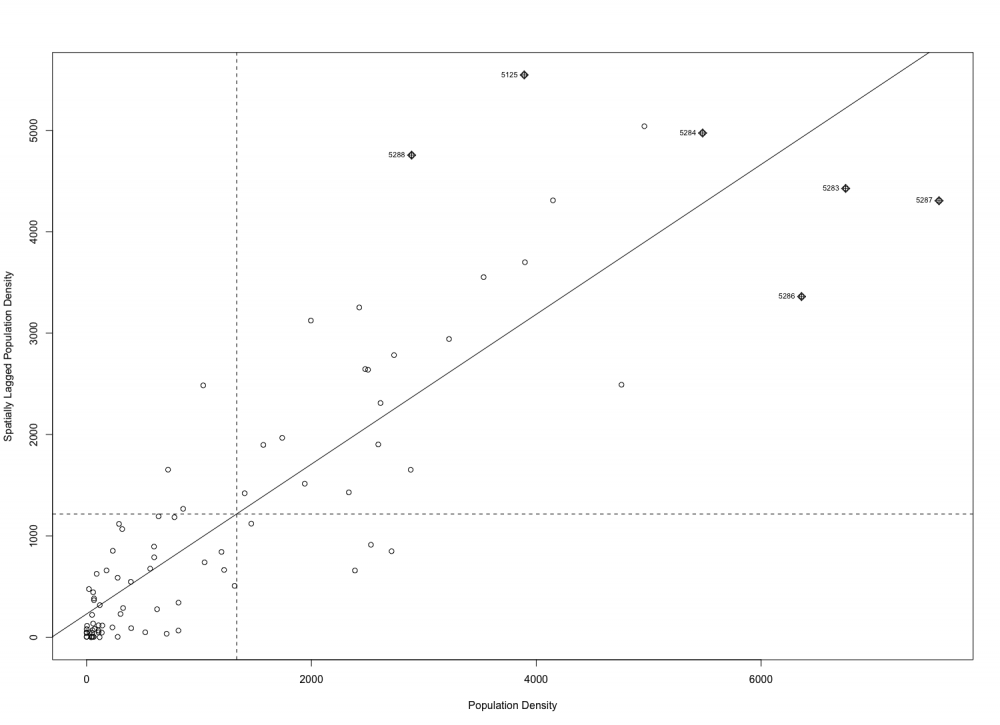
For another method of testing and visualizing spatial autocorrelation, a Moran’s scatterplot can be generated. The x axis of the scatterplot is for the value of the variable standardized to its z-score, and the y axis is the standardized value of neighbor values ( Australian Urban Research Infrastructure Network, n.d.). The scatterplot has four quadrants, and clockwise from the top-right corner they represent high-high, high-low, low-low, and low-high. A positive regression line means most values are low-low and high-high, meaning that when the observed variable has a high value, its neighbors have high values and when the observed variable has low value, its neighbors have low values. This is an indication of positive autocorrelation. If most of the values are low-high or high-low then there would be a negative regression line that is indicative of negative spatial autocorrelation.

Generate a Moran’s I scatterplot using the moran.plot function from the SPDEP package. The function will take weighted list and vector arguments like the Local and Global Moran’s I functions did. We will also include arguments zero.policy, spChk, labels, xlab, and ylab which are used to assign zero values to observations without neighbors, checking the identity integrity of  spatial objects against data vector names, labelling high influence points, labelling the x and y axis, respectively (Bivand, 2017a).

moran.plot(PopDen, crd.lw, zero.policy=NULL, spChk=NULL, labels=NULL, xlab=”Population Density”, ylab=”Spatially Lagged Population Density”)

The regression line of the scatterplot is positive, indicative of a positive autocorrelation where dissemination areas with high values are closer to other areas with high values and areas with low values are closer to other areas with low values. It is noteworthy that there are six points that are labelled as high influence points. It is outside the scope of our tutorial, but a next step for analysis would be to look more specifically at the points of high influence. 

SUMMARY

Using the program R and census data from Canada’s 2016 census, population density in the Capital and Cowichan Valley Regional Districts of Vancouver Island, British Columbia was spatially analyzed. A weighted population density map for the study area was created by generating a neighborhood weights matrix, and multiple method were used to identify spatial autocorrelation. A queen’s case neighborhood matrix was established to create a lagged means map of population density, which was subsequently used as the base map for spatial autocorrelation analysis. The Global Moran’s I method was used to determine if population density values displayed complete spatial randomness, or if the values were positively or negatively spatially autocorrelated. Local Moran’s I was used for mapping to determine where clusters were occurring in population density in the dissemination areas. Local Moran’s I was also used to create a scatterplot to identify outliers and points of high influence. The study found that population density in the Capital and Cowichan Valley Regional Districts was positively spatially autocorrelated, which was confirmed through different methods of inferential testing.

This tutorial demonstrated one method that census data can be used for spatial analysis and to answer questions about places. Census data has multidisciplinary applications, and can be used to answer questions in fields including geology, urban planning, environmental monitoring, epidemiology, or just to answer general questions about the population. Determining spatial autocorrelation can supplement any studies that seek to answer questions about places and place relationships. Spatial autocorrelation is a method of point pattern analysis that allows users to query spatial patterns in data and determine if locations that are closer together are more similar. Using spatial autocorrelation to characterize the distribution of subjects and the patterns of their attributes is a useful spatial analysis tool that all spatial scientists should have in their toolkit.

REFERENCES

Anselin, L. (1995). Local Indicators of Spatial Association – LISA. Geographical Analysis, 27(2), 93-115. DOI: 10.1111/j.1538-4632.1995.tb00338.x

Australian Urban Research Infrastructure Network. (n.d.). Moran’s I Scatterplot. Retrieved from https://docs.aurin.org.au/portal-help/analysing-your-data/chart-tools/moraniscattervisualisation-workflow/

Beale, L. and Mitchell, A. (2015, October 23). How Spatial Analysis Leads to Insight. DataInformed. Retrieved from http://data-informed.com/how-spatial-analysis-leads-to-insight/

Bivand, R. (2017a, September 1). Spdep: Spatial Dependence: Weighting Schemes, Statistics and Models. The Comprehensive R Archive Network. Retrieved from https://cran.r-project.org/web/packages/spdep/index.html

Bivand, R. (2017b, March 25). Maptools: Tools for Reading and Handling Spatial Objects. The Comprehensive R Archive Network. Retrieved from https://cran.r-project.org/web/packages/maptools/index.html

Boragina, N. (2013, November 25). Map with 2011 Census populations of Vancouver Island. Victoria Vision. Retrieved from http://victoriavision.blogspot.ca/2013/11/map-with-2011-census-populations-of.html

Brunsdon, C. and Chen, H. (2014, October 6). GISTools: Some further GIS capabilities for R. The Comprehensive R Archive Network. Retrieved from https://cran.r-project.org/web/packages/GISTools/index.html

Dillon, L. (2010). The value of the Long Form Canadian Census for Long Term National and International Research. Canadian Public Policy, 36(3), 389-393. DOI: 10.3138/cpp.36.3.389

Ditchburn, J. (2010, June 29). Tories scrap mandatory long-form census. The Globe and Mail. Retrieved from https://beta.theglobeandmail.com/news/politics/tories-scrap-mandatory-long-form-census/article4323276/?ref=http://www.theglobeandmail.com&

Eaton, C., Nafziger, A., Strogatz, D. and Pearson, T. (1994). Self-reported physical activity in a rural county: a New York county health census. American Journal of Public Health, 84(1), 29-32. DOI: 10.2105/AJPH.83.1.29

ESRI. (n.d.). Spatial Analysis in GIS Dictionary. Retrieved from http://support.esri.com/en/other-resources/gis-dictionary/term/spatial%20analysis

Fung, J., Lee, C., Chan, M., Seto, W., Lai, C., and Yuen, M. (2015). High prevalence of non-alcoholic fatty liver disease in the Chinese – results from the Hong Kong liver health census. Liver International, 35(2), 542-549. DOI: 10.1111/liv.12619

Gordon-Larsen, P., Nelson, M., Page, P., Popkin, B. (2006). Inequality in the Built Environment Underlies Key Health Disparities in Physical Activity and Obesity. Pediatrics, 117(2), 417-424. DOI: 10.1542/peds.2005-0058

Green, D. and Milligan, K. (2010). The Importance of the Long Form Census of Canada. Canadian Public Policy, 36 (3), 383-388. DOI: 10.3138/cpp.36.3.383

Hijman, R. (2016, June 2). Raster: Geographic Data Analysis and Modeling. The Comprehensive R Archive Network. Retrieved from https://cran.r-project.org/web/packages/raster/index.html

Jerret, M., Finkelstein, M., Brook, J., Arain, M., Kanaroglou, P., Stieb, D., Gilbert, N., Verma, D., Finkelstein, N., Chapman, K., Sears, M. (2009). A Cohort Study of Traffic-Related Air Pollution and Mortality in Toronto, Ontario, Canada. Environmental health perspectives, 117(5), 772-777. DOI: 10.1289/ehp.11533

Lloyd, C. (2010). Spatial Data Analysis: An Introduction for GIS Users. Oxford, UK: Oxford University Press.

Mitrou, F., Cooke, M., Lawrence, D., Povah, D., Mobilia, E., Guimond, E. and Zubrick, S. (2014). Gaps in Indigenous disadvantages not closer: a census cohort study of social determinants of health in Australia, Canada, and New Zealand from 1981-2006. BMC Public Health, 14(1), 201. DOI: 10.1186/1471-2458-14-201.

Sawada, M. (2009). Global Spatial Autocorrelation Indices – Moran’s I, Geary’s C and the General Cross-Product Statistic. University of Ottawa. Retrieved from http://www.lpc.uottawa.ca/publications/moransi/moran.htm

Smith, T. (2015). Spatial Weights Matrices. University of Pennsylvania. Retrieved from https://www.seas.upenn.edu/~ese502/lab-content/extra_materials/SPATIAL%20WEIGHT%20MATRICES.pdf

Statistics Canada. (2011). History of the Census of Canada. Retrieved from http://www12.statcan.gc.ca/census-recensement/2011/ref/about-apropos/history-histoire-eng.cfm

Statistics Canada. (2016a). Census of Population. Retrieved from http://www23.statcan.gc.ca/imdb/p2SV.pl?Function=getSurvey&SDDS=3901

Statistics Canada. (2016b). The aggregate dissemination area (ADA): a new census dissemination geographic area. Retrieved from http://www12.statcan.gc.ca/census-recensement/2016/geo/ADA/adainfo-eng.cfm

University of Pennsylvania State. (n.d.) Choropleth Maps. GEOG 386: Cartography and Visualization. Retrieved from https://www.e-education.psu.edu/geog486/print/book/export/html/1864

Veall, M. 2B or Not 2B? What Should Have Happened with the Canadian Long Form Census? What Should Happen Now? Canadian Public Policy, 36(3), 395-399. Retrieved from http://www.utpjournals.press/doi/full/10.3138/cpp.36.3.395

Voices-Voix. (n.d.) Statistics Canada (mandatory long-form census). Retrieved from http://voices-voix.ca/en/facts/profile/statistics-canada-mandatory-long-form-census

Wickham, H. (2014, January 17). Introducing dplyr. R Studio. Retrieved from https://blog.rstudio.com/2014/01/17/introducing-dplyr/

Wickham, H. (2016, June 8). plyr v1.8.4. RDocumentation. Retrieved from https://www.rdocumentation.org/packages/plyr/versions/1.8.4

Young, L. (2016, May 2). The long-form census is back – here’s what you need to know. Global News. Retrieved from https://globalnews.ca/news/2674538/the-long-form-census-is-back-heres-what-you-need-to-know/

Youngson, N. (Photographer). (2016, August). Census [Digital image]. Retrieved from http://www.thebluediamondgallery.com/wooden-tile/c/census.html